11 Statistisk tolkning
Det vi omtaler som statistisk tolkning eller statistisk inferens handler om å skille systematikk fra støy. Altså: håndtering av usikkerhet ved estimeringen.
- “Bekvemmelighetsutvalg”: Dataene er ikke et tilfeldig utvalg fra noen bestemt populasjon, og det er ikke randomisert til f.eks. kontrollgruppe. I slike utvalg er det ikke den typen usikkerhet ved estimeringen at vi kan regne på usikkerhet på meningsfull måte. Statistisk tolkning er lite relevant.
- Data er et tilfeldig utvalg fra en veldefinert populasjon. Altså: det vi vanligvis mener med “tilfeldig utvalg”. Hvis ikke populasjonen er veldefinert spørs det om det heller er er utvalg av type 2). Usikkerheten er knyttet til tilfeldigheter i hvem som ble med i utvalget. Statistisk tolkning for generalisering gjelder.
- Data er fra et eksperiment eller kvasieksperiment der det er tilfeldig fordeling av hvem som er i behandlingsgruppen og kontrollgruppen (evt. flere grupper). Usikkerhet er knyttet til måling av kausaleffekter, og statistisk tolkning gjelder.
På nivå 2 handler det om å generalisere til en veldefinert populasjon, mens det på nivå 3 handler om å si om en kausal effekten kan skilles fra tilfeldig støy. De statistiske teknikken er imidlertid de samme. I praksis handler dette om følgende:
- standardfeil
- konfidensintervall
- p-verdi
Disse tre henger nøye sammen og er forskjellige uttrykk for feilmarginen ved et estimat. Her skal vi ikke gjennomgå begrunnelsene og det teoretiske grunnlaget for hvordan dette fungerer, men hoppe rett til det praktiske. En skikkelig forklaring følger fra sentralgrenseteoremet1.
Litt enkelt kan vi si at det hvis man gjør en studie på en ordenlig måte, så er ganske sannsynlig at man får en estimat som er lik den sanne verdien. Men det er også ganske lite sannsynlig at man får et estimat som er nøyaktig lik den sanne verdien. Vi må regne med at estimatet avviker noe på grunn av tilfeldigheter! Det er veldig nyttig å vite noe om hvor mye feil man kan forvente å få av tilfeldige grunner. Altså: hva er feilmarginen til den metoden vi bruker til å estimere?
Denne feilmarginen avhenger først og fremst av hvordan undersøkelsen er gjennomført. Utvalgsprosedyren er det viktigste: tilfeldig trukket utvalg er det mest grunnleggende momentet. Hvis det er systematiske skjevheter i dataene, så vil estimatet bli systematisk skjevt på måter vi ikke så lett kan håndtere med statistiske teknikker.
Dernest avhenger feilmarginen av utvalgsstørrelsen. Det er rett og slett slik at større data gir sikrere estimatet. Hvis utvalget består av 10 personer, så vil estimatet være langt mer usikkert enn hvis det hadde bestått av 5000 personer. Selv om det finnes en statistisk forklaring på dette, så er det relativt intuitivt å forstå. I utregninger vil standardfeilen bli mindre hvis antall observasjoner er større.
Til sist avhenger feilmarginen av en grense vi selv setter, som gjerne kalles konfidensgrad. Denne setter vi selv, men det er vanlig å sette denne til 95%. Det gjør at man noen ganger sier “95% sikker”, hvilket er en nokså sleivete måte å si det på, men ikke helt galt under visse forutsetninger som vi kommer tilbake til.
11.1 Stokastiske variabler og sannsynlighetsfordelinger
En stokastisk variabel er en funksjon som tilordner en numerisk verdi til utfallet av et eksperiment. For eksempel, et terningkast er et eksperiment med et utfallsrom som omfatter tallene 1 til 6. Det er usikkerhet knyttet til utfallet av eksperimentet (vi vet ikke på forhånd hva utfallet er, altså om vi kaster 2 eller 5 eller noe annet). La oss si at jeg kaster terningen 100 ganger og teller antall ganger jeg får 6. Vi kan se på denne prosessen som en stokastisk variabel som måler antall 6’ere (den gir utfallet en numerisk verdi).
Hvis vi kaster en vanlig terning, har alle mulige utfall den samme sannsynligheten (1/6). I andre tilfeller, dvs. for andre stokastiske variabler, kan det hende at noen utfall er mer sannsynlige enn andre. Alle stokastiske variabler er derfor forbundet med en tilsvarende sannsynlighetsfordeling. En sannsynlighetsfordeling er en funksjon som tilordner en sannsynlighetsverdi (et tall mellom 0 og 1) til alle mulige verdier av den stokastiske variabelen. Et terningkast følger en binomisk fordeling. Andre fordelinger du kanskje har hørt om er Bernoulli-fordelingen, uniformfordelingen, Poisson-fordelingen og selsvsagt normalfordelingen.
Mini-oppgave: Kan du tenke på og forklare hvordan en survey er et stokastisk utfall (en realisering) av et eksperiment?
11.1.1 Estimater som stokastiske variabler
Når vi produserer statistiske estimater, er vi som oftest avhengige av et (tilfeldig) utvalg fra en større populasjon (vi måler som regel utdanningsnivået til et utvalg mennesker, ikke for hele befolkningen). Dette betyr at et estimat kan variere fra ett utvalg til et annet: det er usikkerhet knyttet til det. Med andre ord, kan selve estimatet anses som en stokastisk variabel. Med nok observasjoner, forteller sentralgrenseteoremet at denne stokastiske variabelen følger en normalfordeling med to viktige parametere: en gjennomsnittlig (forventet) verdi og en varians. Denne variansen kvantifiserer hvor mye estimatene våre kan variere dersom vi trekker et nytt (hypotetisk) utvalg fra populasjonen. I praksis, forholder vi oss som regel til standardavviket og ikke variansen til denne utvalgsfordelingen. Standardavviket til denne fordelingen kalles standardfeilen (se under).
Standardfeilen forbundet med et estimat kan brukes til å bygge et konfidensintervall (se under). Dette er et intervall som med en gitt sannsynlighet inneholder den sanne verdien av det vi prøver å estimere (gitt antakelsene som vår statistiske modell legger til grunn). Et 95 prosent konfidensintervall er definert som et intervall som gjennom hypotetisk repeterte datasamlinger, “fanger” denne sanne verdien med 95 prosent sannsynlighet. Som en røff tommelfingerregel, tilsvarer et slikt intervall estimatet ± 2 ganger standardfeilen.
Mini-oppgave: Gitt det du vet om normalfordelingen, forklar hvorfor vi er 95 prosent sikre på at den sanne verdien til det vi estimerer faller innenfor ca. 2 ganger standardfeilen.
11.2 Estimater og feilmarginer
11.2.1 Estimat
La oss si at du ønsker å si noe om gjennomsnittet i populasjonen, men har bare data om et tilfeldig utvalg fra denne populasjonen. Når du da regner ut gjennomsnittet i utvalget er det din beste gjetning på hva gjennomsnittet er i populasjonen. En slik gjetning kaller vi et estimat.
11.2.2 Standardfeil
Standardfeilen uttrykker usikkerheten ved estimatet. Standardfeilen til estimatet er et mål på usikkerheten ved målemetoden. Usikker målemetode gjør at feilen kan være større.
Ordet standardfeil er lett å blande sammen med standardavvik i mer generell forstand, så la oss ta det med det samme. Standardavviket beskriver som regel variasjon i observerte data, f.eks. hvis man vil beskrive hvordan personers inntekt varierer rundt gjennomsnittet. Standardavviket beskriver altå variasjon i data.
Standardfeilen beskriver derimot ikke data, men sannsynlighetsfordelingen for hvordan vi forventer at estimatet vil kunne avvike fra den sanne verdien på grunn av tilfeldigheter.
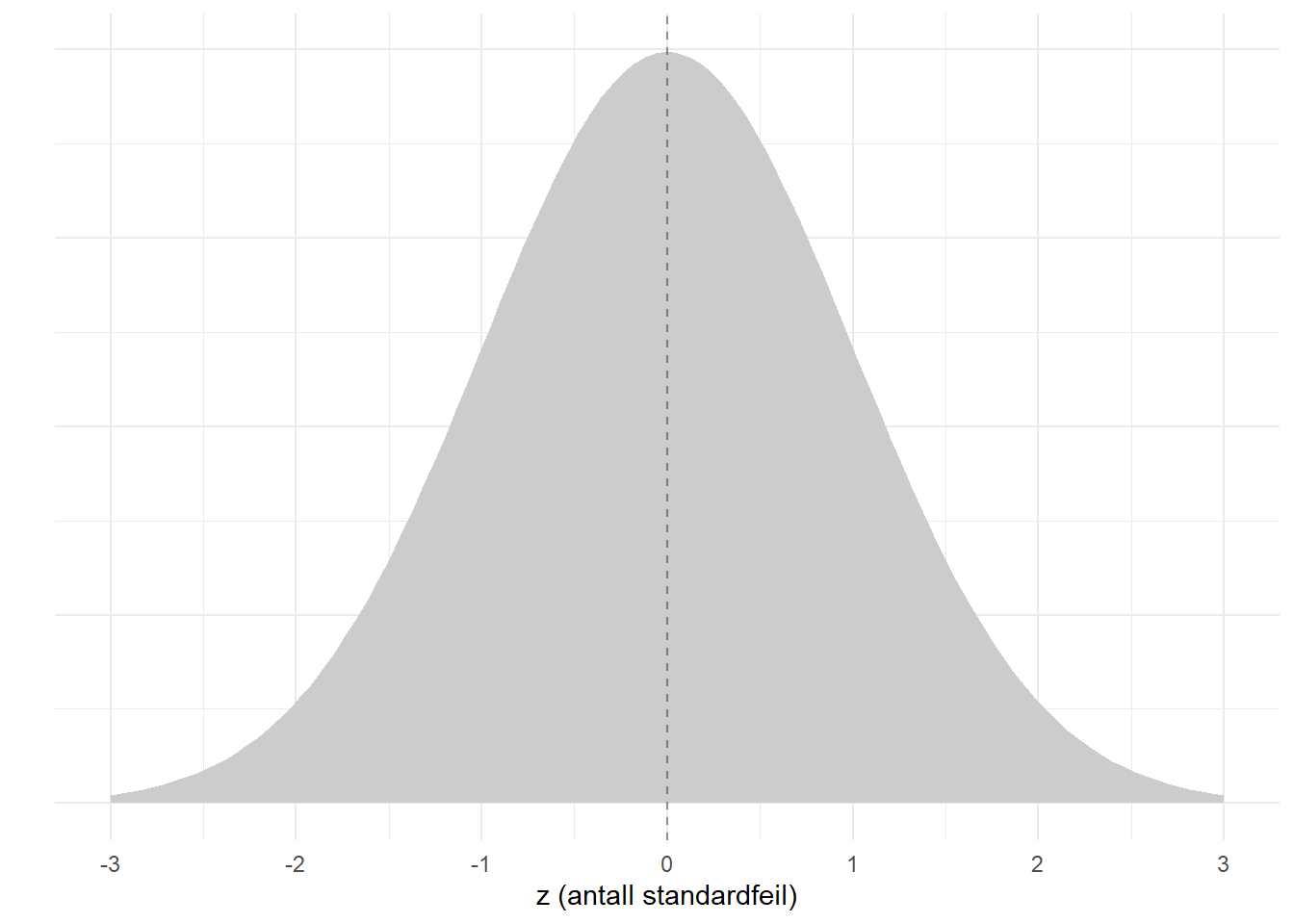
Sentralgrenseteoremet sier at estimatet på et gjennomsnitt vil ha tilfeldige feil som er normalfordelt, og dermed kan vi bruke normalfordelingen til å si noe om usikkerheten ved estimatet. Dette er forsøkt illustrert nedenfor der x-aksen viser hvor mye estimatet kan avvike fra den sanne verdien, mens kurven viser hvor sannsynligsfordelingen til avviket. Den stiplede linjen viser den sanne verdien. Når x-aksen er avvik fra sanne verdien, så vil altså \(x = 0\) bety null avvik fra sanne verdien: helt riktig estimat.
Altså: det er aller mest sannsynlig å få et estimat som ligger nærme den sanne verdien, men litt avvik (større eller lavere estimat) er nesten like sannsynlig. Jo lengre til hver av sidene man går (større feil), jo mindre sannsynlig er det å få et slikt estimat.
Skalaen på x-aksen er \(z\), som i denne sammenheng kan tolkes som antall standardfeil. Den følger en standard normalfordeling som har kjente og faste egenskaper. Vi vet f.eks. at andelen nedenfor -1.96 er 0.025, og det samme gjelder ovenfor 1.96. Dette er illustrert i figuren nedenfor. Det er altså 0.05 (dvs 5%) sannsynlighet for å få et estimat som ligger 1.96 standardfeil unna den sanne verdien. Motsatt er sannsynligheten for å få et estimatet innenfor intervallet mellom -1.96 og 1.96 tilsvarende 95%. Dette er grunnlaget for det vi kaller konfidensintervall.
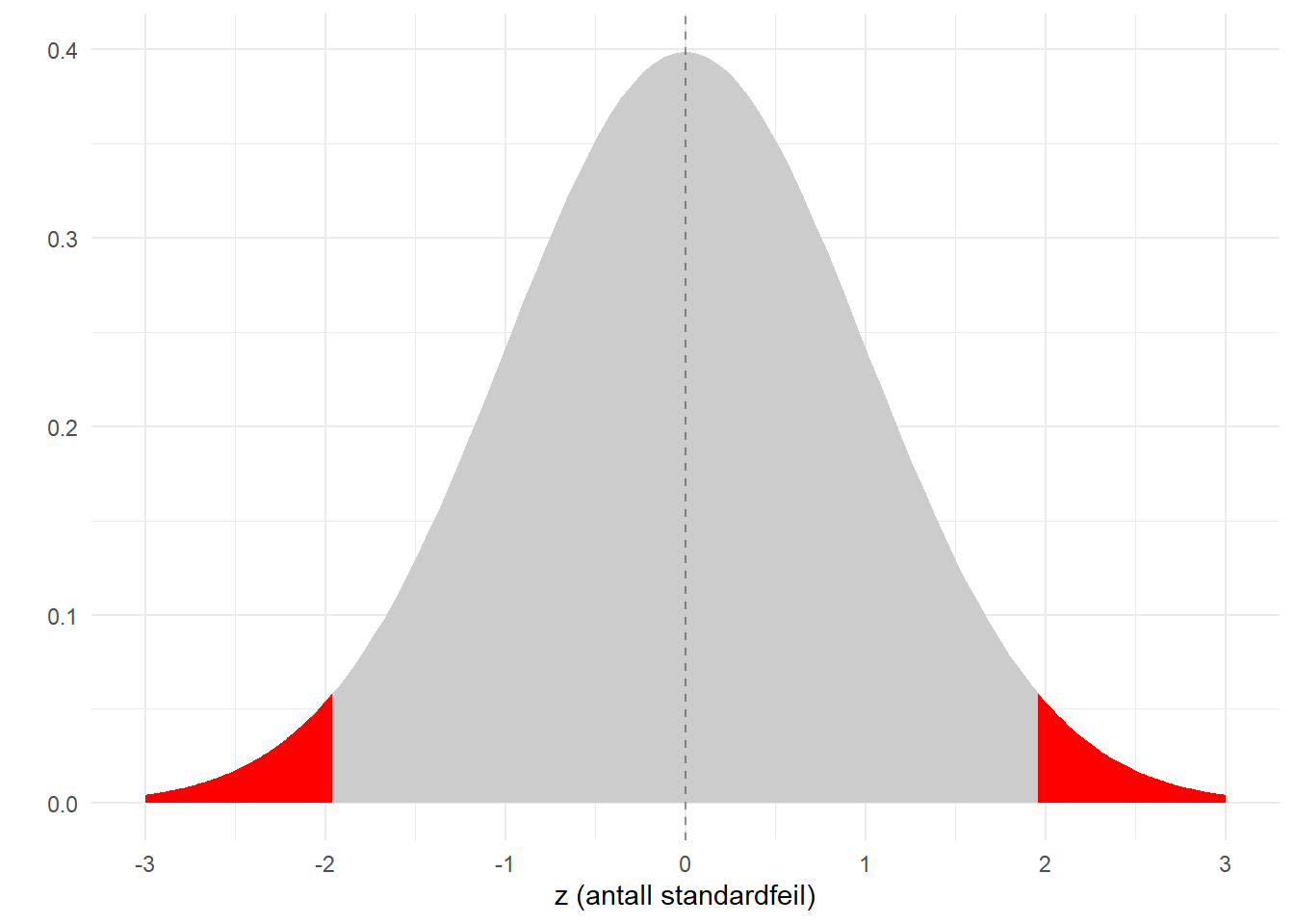
11.2.3 Konfidensintervall
Hvis man ønsker å være “95% sikker”, så bruker man altså et 95% konfidensintervall. Det er ikke noe magisk ved akkurat 95% og er primært blitt en norm. Grunnen er bare at det skal være en ganske lav sannsynlighet for at estimatet skyldes tilfeldig variasjon.
Til ethvert estimat er knyttet en feilmargin som uttrykkes ved \(z \times se\), der \(se\) er forkortelse for standardfeil (engelsk: “standard error”). \(z\) er et tall som er knyttet til grad av usikkerhet ved feilmarginen. En feilmargin basert på 95% konfidensgrad er dermed \(1.96 \times se\). Hvis man så tar denne feilmarginen til hver side, så gir det samme som illustrert i figuren ovenfor.
Et konfidensintervall er altså bare å ta hensyn til feilmarginen til hver side av estimatet. Når vi bruker dette i praksis baserer vi oss på denne normalfordelingen og trenger bare å få regnet ut standardfeilen i tillegg.
[1] 91.0712Hvis man f.eks. har estimert gjennomsnittlig timelønn til å være 90.2 og standardfeilen er 0.5. Da blir 95% konfidensintervallet som følger:
\[ 90.1 \pm 1.96 \times 0.47 = [89.2, 91.1]\] Dette betyr at vi har brukt en målemetode som har en feilmargin som gjør at vi kan være 95% sikker på at den sanne verdien ligger innenfor dette intervallet.
11.2.3.1 Er man egentlig “95% sikker”?
Det sies ofte at feilmarginen uttrykker hvor sikker man er. Det er jo ikke helt riktig - eller det er riktig under noen spesielle forutsetninger om hva man mener med “sikker”. La oss derfor ta dette med en gang.
Et 95% konfidensintervall er vårt anslag på hvor god vår målemetode er. Vi har jo regnet ut f.eks. et gjennomsnitt og det er jo greit nok. Usikkerheten kommer fra utvalgsprosedyren og variasjonen i data.
Vi vet ikke hvorvidt vårt estimat ligger nærme eller langt unna den sanne verdien. Det vi derimot vet noe om er påliteligheten i den metoden vi har brukt. Det viktigste her er altså tilfeldig utvalg, og hvis utvalget ikke er tilnærmet tilfeldig trukket, så bryter det hele sammen.
Når man sier at konfidensintervallet uttrykker at man er “95% sikker” på at den sanne verdien ligger i det intervallet mener man da følgende: Man har brukt en metode (dvs utvalg og utregninger og det hele) som har en feilmargin. Denne feilmarginen er slik at hvis man gjorde estimeringen (altså nytt utvalg hver gang) på samme måte svært mange ganger (f.eks. uendelig mange ganger), så ville 95% av resultatene ligget innenfor et slikt intervall.
Man gjør selvsagt ikke samme undersøkelse tusenvis av ganger, så dette er en hypotetisk tanke. Man man kan også tenke seg at mange ulike forskere gjør en tilsvarende studie og får litt forskjellige resultat. Disse resultatene vil (i teorien) fordele seg som en normalfordeling rundt den sanne verdien. Noen ganske få vil ligge langt unna sannheten.
11.2.4 T-testen
Hvis man skal sammenligne to grupper, så vet vi i utgangspunktet at dataene fra et utvalg antakeligvis vil vise at de ikke er helt like på grunn av tilfeldig variasjon. Det kan altså være at gruppene er like i virkeligheten, bare at dataene våre tilfeldigvis ble litt forskjellige. Det må vi jo regne med, men det er begrenset hvor forskjellig vi kan forvente at gruppene er på grunn av rene tilfeldigheter.
Se igjen på figuren over av normalfordelingen i omtalen av konfidensintervall. Gitt at det ikke er noen sann forskjell mellom gruppene, så vil vi forvente at estimatet ligger innenfor en viss feilmargin. Det betyr at en observert forskjell i dataene som ligger innenfor denne feilmarginen vil være konsistent med at forskjellene bare skyldes tilfeldig variasjon. Motsatt: hvis estimatet ligger utenfor denne feilmarginen, ja da kan vi si at det ikke er konsistent med dette utgangspunktet om at forskjellene bare skyldes tilfeldig variasjon.
En av de meste brukte statistiske testene i praksis er “t-testen”. Du kan tenke på det som en beslutningsregel: hva skal til for at du skal bestemme deg for å tro at forskjellen ikke skyldes tilfeldigheter? Standardfeil og feilmarginer er det samme som før, så du må bare bestemme deg for hvor stor feilmargin du er villig til å operere med. Hvis estimatet på en differanse er større enn feilmarginen, da forkastes hypotesen om at forskjeller skyles tilfeldigher. Altså: forskjellene i data må da skyldes noe mer systematisk.
Så i utgangspunktet så må du altså ta stilling til om du mener det er en forskjell - eller ikke. Du kan ikke konkludere med at det “kanskje er en forskjell”, men må ta et valg. Derfor kaller vi gjerne dette for hypotesetesting i en litt snever forstand. Det er bare to mulige hypoteser:
\(H_0\): Det er egentlig ingen forskjell mellom gruppene, og forskjell i dataene skyldes bare tilfeldig variasjon. (Nullhypotesen). \(H_A\): Det er faktisk en forskjell mellom gruppene, og forskjellen i dataene er for stor til av det er sannsynlig at det skyldes tilfeldig variasjon. (Alternativ hypotese).
11.2.4.1 Formler og slikt
T-testen i prinsippet en sammenligning mellom estimatets størrelse og standardfeilen til estimatet. Vi kan skrive det som følger:
\[ \frac{\mu}{SE(\mu)} = t \]
Eller sagt på en annen måte: \[ \frac{estimat}{standardfeil} = t \]
Det betyr at \(t\)-verdien egentlig bare er forholdstallet mellom estimatet og standardfeilen. Intuitivt kan man vel forstå at hvis usikkerheten bør være mindre enn estimatet. Altså: hvis du har estimert en forskjell i timelønn mellom to grupper, og feilmarginen til dette estimatet er større enn forskjellen, ja, da er det vanskelig å lære noe særlig fra det estimatet.
Verdien \(t\) tilsvarer verdien \(z\) som vi nevnte i forbindelse med konfidensintervall. Så hvis \(t\) er større enn \(z\), så ligger estimatet utenfor konfidensintervallet.
Tolkningen av \(t\)-verdien brukes gjerne som en en beslutningsregel: Ja/Nei. Litt firkantet, med andre ord. Men \(t\)-verdien er også knyttet til normalfordelingen på samme måte som nevnt ovenfor i forbindelse med konfidensintervaller. Ethvert mulig resultat er knyttet til en viss sannsynlighet for at det skal skje ved en tilfeldighet.
11.2.4.2 P-verdi
Tolkningen av p-verdien er i hvilken grad det er sannsynlig å få det observerte resultatet ved en tilfeldighet hvis NULL-hypotesen er riktig. Dette høres ganske pussig ut. Tanken er at man nesten alltid vil observere noe forskjell fra null, og det kan skje ved en tilfeldighet. Hvis null-hypotesen er riktig er det mindre sannsynlig at vi observerer en veldig stor forskjell. Men hvor stor forskjell er det, egentlig? Løsningen er å se avstanden fra null i lys av standardfeilen. Hvis man bruker en usikker målemetode, så er det mer sannsynlig å observere en stor forskjell ved tilfeldigheter enn om man bruker en veldig nøyaktig målemetode.
I praksis: Tenk at du observerer en stor forskjell mellom to grupper. Med “stor” mener vi f.eks. at forskjellen er over dobbelt så stor som standardfeilen. Da får vi en p-verdi som er \(p < 0.05\). Da kan vi si at hvis nullhypotesen er sann, så er det lite sannsynlig at vi ville fått et slikt resultat på grunn av tilfeldigheter.^(Hvis vi ønsker være pinlig korrekte kan vi også si noe slikt som at hvis man gjorde målingen tusenvis av ganger, så ville 5% av resultatene ligge så langt unna null (eller lengre).)
Så er logikken videre at vi som hovedregel ikke tror på resultater som er usannsynlige. Så i stedet for å holde fast på nullhypotesen velger vi i stedet å tro på den alternative hypotesen.
11.3 Kan man velge fritt konfidensgrad?
Det er ingenting magisk med tallet 1.96 eller \(p < 0.05\). Det er en konvensjon. Konfidensgrad er nemlig noe du velger. All tolkning av “statistisk signifikans” er basert på en gitt konfidensgrad.
Problemet oppstår hvis du først ser på resultatene og så velger en konfidensgrad som passer til det du har mest lyst til å konkludere med. Det er rett og slett juks. For at du skal velge en annen konfidensgrad må du si det høyt og tydelig før du gjennomfører undersøkelsen - og da må du faktisk etterleve det når resultatene foreligger. Du bør også kunne argumentere selvstendig for en annen konfidensgrad, altså før resultatene foreligger. Dette innebærer at det ikke er godt nok å si det høyt ut i luften der du sitter alene for deg selv. Det må pre-registeres på et offentlig sted, f.eks. osf.io eller tilsvarende websider.
Dette er egentlig en mye større diskusjon, men verd å være obs på. Du kan velge konfidensgrad, men i så fall må du gjøre det på en ordenlig måte hvis du vil bli tatt seriøst av andre. Vi skal ikke drive med cherry-picking av resultater og konklusjoner!
11.4 Statistiske tester generelt
Det finnes en hel haug av statistiske tester. Prinsippet er gjerne variasjoner av t-testen og har disse komponentene:
- en nullhypotese og et alternativ
- en statistikk, altså et måltall som er et avstandsmål mellom observert resultat og hva man forventer under nullhypotesen
- en statistisk modell for samplingfordelingen som sier noe om fordelingen av tilfeldige feil
- en uttalt beslutningsregel for konklusjonen. Et vanlig mål er at hvis \(p < 0.05\), så forkastes nullhypotesen.
Du har sikker lært om \(\chi^2\) testen for krysstabeller. Den er forskjellig på mange måter fra \(t\)-testen, men logikken er tilsvarende: \(\chi^2\) er et avstandsmål for hva vi forventer gitt hypotesen om ingen forskjell. Hvis resultatet fra dataanalysen er for langt unna dette, så beslutter vi å tro at forskjellen skyldes systematikk.